Let the required point on the curve y = \(\sqrt{x - 3}\) be P(x1, y1).
Differentiating y = \(\sqrt{x - 3}\) w.r.t. x, we get
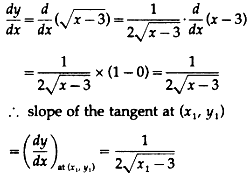
Since, this tangent is perpendicular to 6x + 3y - 5 = 0
whose slope is -6/3 = -2,
slope of the tangent = -1/-2 = 1/2

Hence, the required points are (4, 1) and (4, -1).