Correct option is (A) 96
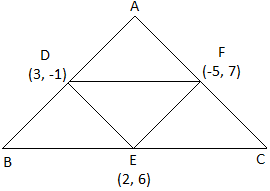
Let \(D(3,-1),E(2,6)\;and\;F(-5,7)\) are mid-points of sides AB, BC & AC respectively.
\(\therefore\) Area of \(\triangle ABC\) \(=4\times\) Area of \(\triangle DEF\)
Now, area of \(\triangle DEF\) \(=\frac12|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|\)
\(=\frac12|3(6-7)+2(7-(-1))+(-5)(-1-6)|\)
\(=\frac12|3\times-1+2\times8-5\times-7|\)
\(=\frac12|-3+16+35|\)
\(=\frac12\times48=24\) square units
\(\therefore\) Area of \(\triangle ABC\) \(=4\times\) Area of \(\triangle DEF\)
\(=4\times24=96\) square units