Consider a particle moving along a circular path of constant radius r. If the particle is speeding up or slowing down, its motion is nonuniform, and its angular speed ω and linear speed v both change with time. At any instant, v, ω and r are related by v = ωr The angular acceleration of the particle is α = \(\frac{d \omega}{dt}\)
The tangential acceleration is the linear acceleration \(\vec{a_t}\) that produces a change in the linear speed of the particle and is tangent to the circle. In magnitude,
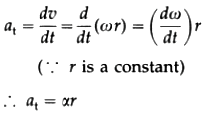
This is the required relation.