Question

AB is a chord of length 24 cm of a circle of radius 13 cm. The tangents at A and B intersect at a point C. Find the length AC.

(A) 31.2 cm

(B) 12 cm

(C) 28.8 cm

(D) 25 cm

Answer 1

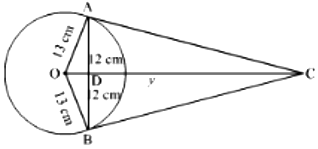
Let O be the centre of the circle and AB and OC intersect at D

Now let CD = y

Since OC is the perpendicular bisector of AB

\(\therefore\) AD = BD 

= \(\frac{24}2\) cm

= 12 cm

In right \(\triangle\)OAP

OA² = AD² + OD²

⇒ OD² = OA² - AD²

= (13 cm)² - (12 cm)²

= 169 cm² - 144 cm²

= 25 cm²

⇒ OD = \(\sqrt{25 \,cm^2}\) = 5 cm

In right triangle's OAC and ADC

AC² = AD² + DC²

OC² = OA² + AC²

⇒ OC² = OA² + (AD² + DC²) 

⇒ (CD + OD)² = (13 cm)² + (12 cm)² + y²

⇒ (y + 5 cm)² = 169 cm² + 144 cm² + y²

⇒ y² + 10y cm + 25 cm² = 313 cm² + y²

⇒ 10y = (313 - 25) cm = 288 cm

⇒ y = \(\frac{288}{10} =\frac{144}5\) cm

⇒ CD = 28.8 cm²

\(\therefore\) AC² = AD² + DC²

\(=(12 \,cm)^2 + (\frac{144}5 \,cm)^2\)

\(= 144 \,cm^2 + \frac{20736}{25}\, cm^2\) 

\(= \frac{3600 \,cm^2 + 20736\, cm^2}{25}\)

\(= \frac{24336}{25} cm^2\)

\(= (\frac{156}{5} cm)^2\) 

Hence,

AC = \(\frac{156}5\) = 31.2 cm.

Answer 2

The correct option is: (A) 31.2 cm

Explanation:

Given,

Chord AB = 24 cm,

Radius OB - OA - 13 cm.

=> AC = BC = 31 .2 cm

=> AC = BC = 31.2 cm