Solution:
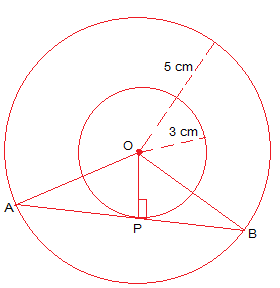
Let the two concentric circles with centre O.
AB be the chord of the larger circle which touches the smaller circle at point P.
∴ AB is tangent to the smaller circle to the point P.
⇒ OP ⊥ AB
By Pythagoras theorem in ΔOPA,
OA2 = AP2 + OP2
⇒ 52 = AP2 + 32
⇒ AP2 = 25 - 9
⇒ AP = 4
In ΔOPB,
Since OP ⊥ AB,
AP = PB (Perpendicular from the center of the circle bisects the chord)
AB = 2AP = 2 × 4 = 8 cm
∴ The length of the chord of the larger circle is 8 cm.