Solution:
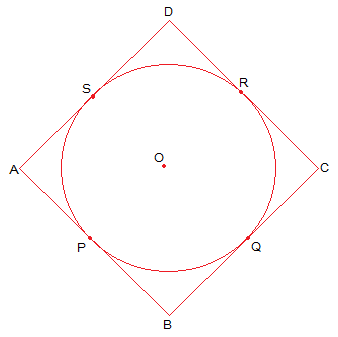
ABCD is a parallelogram,
∴ AB = CD ... (i)
∴ BC = AD ... (ii)
From the figure, we observe that,
DR = DS (Tangents to the circle at D)
CR = CQ (Tangents to the circle at C)
BP = BQ (Tangents to the circle at B)
AP = AS (Tangents to the circle at A)
Adding all these,
DR + CR + BP + AP = DS + CQ + BQ + AS
⇒ (DR + CR) + (BP + AP) =
(DS + AS) + (CQ + BQ)
⇒ CD + AB = AD + BC ... (iii)
Putting the value of (i) and (ii) in equation (iii) we get,
2AB = 2BC
⇒ AB = BC ... (iv)
By Comparing equations (i), (ii), and (iv) we get,
AB = BC = CD = DA
∴ ABCD is a rhombus.