Question

Lines 5x + 12y -10 = 0 and 5x - 12y - 40 = 0 touch a circle C₁ of diameter 6. If the centre of C₁ lies in the first quadrant, find the equation of the circle C₂ which is concentric with C₂ and cuts intercepts of length 8 on these lines.

Answer 1

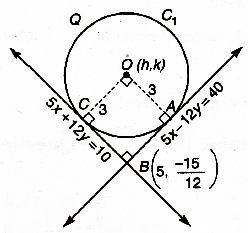
Since, 5x + 12y -10 = 0 and 5x - 12y - 40 = 0 are both perpendicular tangents to the circle C₁ 

. ^.. OABC forms a square

Let the centre coordinates be (h, k) where, OC = OA = 3 and OB = 6√2.

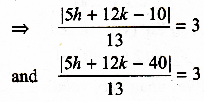
=> 5h + 12k -10 = ±39 and 5h - 12k - 40 = ± 39 on solving above equations. The coordinates which lie in I quadrant are (5, 2).

.'. Centre for C₁ (5, 2)

To obtain equation of circle concentric with C₁ and making an intercept of length 8 on 5x + 12y = 10 and 5x - 12y = 40

=> required equation of circle C₂ has centre (5, 2) and radius 5

=> (x - 5)² + (y - 2)² = 5²