Question

A chord of a circle of radius 12 cm. subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle.

Answer 1

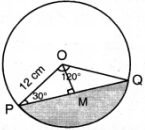
Radius of the circle r = 12 cm. 

Area of the sector = \(\frac{x}{360}\) × πr 

Here, x = 120°

\(\frac{120 }{360}\)× 3.14 × 12 × 12 = 150.72 

Drop a perpendicular from ‘O’ to the chord PQ. 

△OPM = △OQM [∵ OP = OQ ∠P = ∠Q; angles opp. to equal sides OP & OQ; ∠OMP = ∠OMQ by A.A.S] 

∴ △OPQ = △OPM + △OQM = 2 . △OPM 

Area of △OPM = 1/2 × PM × OM

= 18 × 1.732 = 31.176 cm 

∴ △OPQ = 2 × 31.176 = 62.352 cm 

∴ Area of the minor segment = (Area of the sector) – (Area of the △OPQ) 

= 150.72 – 62.352 

= 88.368 cm²