Question

Find the coordinates of points which trisect the line segment joining (1, – 2) and (– 3, 4).

Answer 1

Let A (1, –2) and B(–3, 4) be the given points. Let the points of trisection be P and Q. 

Then AP = PQ = QB = λ (say)

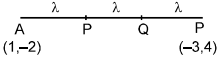
∴ PB = PQ + QB = 2λ and AQ = AP + PQ = 2λ 

⇒ AP : PB = λ : 2λ = 1 : 2 and AQ : QB = 2λ : λ = 2 : 1 

So P divides AB internally in the ratio 1 : 2 while Q divides internally in the ratio 2 : 1