Question

Find the coordinates of the points which trisect the line segment joining the points (2,3) and (6,5).

Answer 1

Let P and Q be the points of trisection of AB, i.e. AP = PQ = QB

∴ P divides AB internally in the ratio 1: 2.

∴ the coordinates of P, by applying the section formula, are

Here, m₁ = 1, m₂ = 2

(x₁, y₁) = (2, 3) and (x₂, y₂) = (6, 5)

Putting the above values in the above formula, we get

Now, Q also divides AB internally in the ratio 2: 1. So, the coordinates of Q are

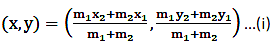
Here, m₁ = 2, m₂ = 1

(x₁, y₁) = (2, 3) and (x₂, y₂) = (6, 5)

Putting the above values in the above formula, we get

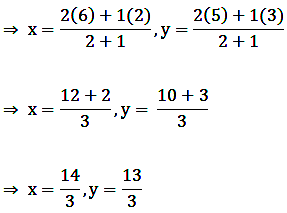
Therefore, the coordinates of the points of trisection of the line segment joining A and B are (10/3, 11/3) and (14/3, 13/3).