AC circuit with a pure capacitance

Consider an AC circuit with a pure capacitance C as shown in the figure. The alternating voltage v is given by
\(v=v_{m}\,sin(\omega t)=>\bar V=V_{m}\angle 0^\circ\)----------(1)
The current flowing in the circuit is i. The voltage across the capacitor is given as VC which is the same as v .
We can find the current through the capacitor as follows
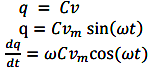
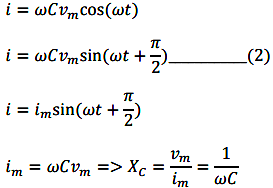
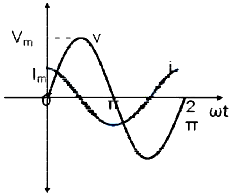
From equation (1) and (2) we observe that in a pure capacitive circuit, the current leads the voltage by 90⁰. Hence the voltage and current waveforms and phasors can be drawn as below.

Capacitive reactance
The capacitive reactance XC is given as
\(X_{c}=\frac{1}{2\pi fC}\)
\(i_{m}=\frac{v_{m}}{X_{c}}\)
It is equivalent to resistance in a resistive circuit. The unit is ohms ( )

