Question

Find the area of triangle ABC with A(1, -4) and the mid points of sides through A being (2, -1) and (0, -1).

Answer 1

Let the coordinates of vertices B be (x₂, y₂) and C be (x₃, y₃)

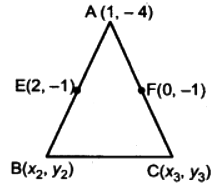
Let E (2, – 1) and F (0, – 1) are mid points of AB and AC respectively.

∴ 2 = 1+x₂/2 and -1 = −4+y₂/2

⇒ 4 = 1 + x₂ and -2 = -4 + y₂

⇒ x₂ = 3 and y₂ = 2

∴ (x₂, y₂) = (3, 2)

Again 0 = 1+x₃/2 and -1 = −4+y₃/2

⇒ 0 = 1 + x₃ and -2 = -4 + y₃

⇒ x₃ = -1 and y₃ = 2

⇒ (x₃, y₃) = (- 1, 2)

Here, x₁ = 1, y₁ = -4, x₂ = 3,

y₂ = 2, x₃ = – 1, y₃ = 2

Area of ABC = 1/2[x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃ (y₁ – y₂)]

= 1/2[1(2 – 2) + 3(2 + 4) + (-1)(-4 – 2)]

= 1/2[1 × 0 + 3 × 6 + (-1) × (-6)]

= 1/2[0 + 18 + 6] = 1/2 × 24 = 12

Hence, area of ABC = 12 sq.units