Let the area of the region {(x, y): x − 2y + 4 ≥ 0, x + 2y^2 ≥ 0, x + 4y^2 ≤ 8, y ≥ 0} be m/n,

Question

Let the area of the region \(\{(x, y): x-2 y+4 \geq 0, \left.x+2 y^{2} \geq 0, x+4 y^{2} \leq 8, y \geq 0\right\}\) be \(\frac{m}{n}\), where m and n are coprime numbers. Then m + n is equal to _____.

Answer 1

Correct answer: 119

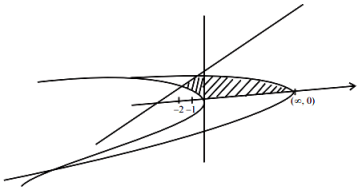
\(\mathrm{A=\int_{0}^{1}\left[\left(8-4 y^{2}\right)-\left(-2 y^{2}\right)\right] d y+\int_{1}^{3 / 2}\left[\left(8-4 y^{2}\right)-(2 y-4)\right] d y}\)

\(=\left[8 \mathrm{y}-\frac{2 \mathrm{y}^{3}}{3}\right]_{0}^{1}+\left[12 \mathrm{y}-\mathrm{y}^{2}-\frac{4 \mathrm{y}^{3}}{3}\right]_{1}^{3 / 2}=\frac{107}{12}=\frac{\mathrm{m}}{\mathrm{n}}\)

\(\therefore \mathrm{m}+\mathrm{n}=119\)