Let two straight lines drawn from the origin O intersect the line 3x + y = 12 at the points P and Q such that

Question

Let two straight lines drawn from the origin O intersect the line \(3 x+4 y=12\) at the points P and Q such that \(\triangle \mathrm{OPQ}\) is an isosceles triangle and \(\angle \mathrm{POQ}=90^{\circ}\). If \(l=\mathrm{OP}^{2}+\mathrm{PQ}^{2}+\mathrm{QO}^{2}\), then the greatest integer less than or equal to \(l\) is :

(1) 44

(2) 48

(3) 46

(4) 42

Answer 1

Correct option is (3) 46

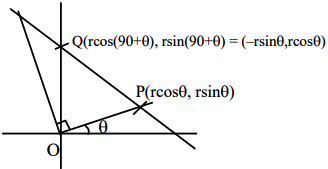
\(3 x+4 y=12\)

\(3(\mathrm{r} \cos \theta)+4(\mathrm{r} \sin \theta)=12\)

\(\mathrm{r}(3 \cos \theta+4 \sin \theta)=12 \quad....(1)\)

\(3(-r \sin \theta)+4(\mathrm{r} \cos \theta)=12\)

\(\mathrm{r}(-3 \sin \theta+4 \cos \theta)=12 \quad ....(2)\)

\(\left(\frac{12}{\mathrm{r}}\right)^{2}+\left(\frac{12}{\mathrm{r}}\right)^{2}=(3 \cos \theta+4 \sin \theta)^{2}+(-3 \sin \theta+4 \cos \theta)^{2}\)

\(2\left(\frac{12}{\mathrm{r}}\right)^{2}=9+16\)

\(\frac{2 \times 144}{\mathrm{r}^{2}}=25 \Rightarrow 288=25 \mathrm{r}^{2}\)

\(\Rightarrow \frac{288}{25}=\mathrm{r}^{2}\)

\(\Rightarrow \sqrt{2}\left(\frac{12}{5}\right)=\mathrm{r}\)

\(l=\mathrm{OP}^{2}+\mathrm{PQ}^{2}+\mathrm{QO}^{2}\)

\(l=\mathrm{r}^{2}+\mathrm{r}^{2}+\mathrm{r}^{2}(\cos \theta+\sin \theta)^{2}+\mathrm{r}^{2}(\sin \theta+\cos \theta)^{2}\)

\(=2 \mathrm{r}^{2}+\mathrm{r}^{2}(1+\sin 2 \theta+1-2 \sin 2 \theta)\)

\(=2 \mathrm{r}^{2}+2 \mathrm{r}^{2}\)

\(=4 \mathrm{r}^{2}\)

\(=4\left(\frac{288}{25}\right)\)

\(=\frac{1152}{25}\)

\(=46.08\)

\([l]=46\)