Question

Explain the concept of temperature, pressure of an ideal gas and Graham diffusion law, on the basis of kinetic theory of gases.

Answer 1

From ideal gas equation,

\(PV = RT\ ..(1)\) 

From equations  (1)

where k_B is Boltzmann's constant. From equation (3),

\(\frac{1}{2}m\overline{v^2}\propto \ T\ ..(4)\)

This means that the average kinetic energy of a molecule is proportional to the absolute temperature of the gas. It is independent of pressure, volume or nature of the ideal gas. This is a fundamental result that relates temperature (a macroscopic measurable of a gas) to the average kinetic energy of a molecule (a molecular quantity). Equation  tells us that the internal energy of an ideal gas depends only upon temperature, and not on pressure or volume. From this, we can say that the kinetic theory of an ideal gas is completely consistent with the ideal gas equation and with the different laws based on it. For a mixture of non-reactive ideal gases, the total pressure gets the contribution from all of the gas in the mixture. Equation becomes

\(P = \frac{1}{3}\left(n_1m_1\overline{v_1^2} + n_2m_2\overline{v_2^2} + ...\right)\ ...(5)\) 

In equilibrium, the average kinetic energy of the molecules of different gases will be equal, i.e.,

\(\frac{1}{2}m_1\overline{v_1^2} = \frac{1}{2}m_2\overline{v_2^2} = \frac{3}{2}k_BT\) 

P = (n₁ + n₂ + ....) k_B T ........(6)

This is Dalton’s law of partial pressures.

From equation (3), the root mean square speed of a molecule in nitrogen gas at temperature, T = 300 K can be calculated as:

\(\overline{v^2}\) is root mean square (rms) speed and is denoted by v_rms.

So, v_rms = 516 m s^-1

The speed is of the order of speed of sound in air. From equation (13.20), it is followed that lighter molecules have greater rms speed, at the same temperature.

Graham’s Diffusion Law

According to Graham’s thffusion law, at equal pressure. the rate of diffusion (r) for a gas and the square root density of gas (p) are inversely proportional to each other, i.e.,

\(r\propto\frac{1}{\sqrt{\rho}}\)

According to kinetic theory of ideal gases, pressure of gas and mean square speed \(\left(\overline{v^2}\right)\) are related as:

So, if pressures are equal. Then

\(V_{rms}\propto\sqrt{\frac{1}{\rho}}\ ....(8)\)

Since the rate of diffusion will be directly proportional to the root mean square speed (v_rms), i.e.,

r ∝ v_rms .........(9)

Then, from equations (8) and (9),

\(r\propto\frac{1}{\sqrt{\rho}}\ ...(10)\)

This is Graham's diffusion law.

If two gases A and B at same pressure have mean square speeds of \(\overline{v_1^2}\) and \(\overline{v_2^2}\) respectively, and ρ₁ and ρ₂ are densities respectively, then from equation (11),

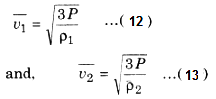
Then, from equations (12) and (13),

\(\frac{v_1}{v_2} = \sqrt{\frac{\rho _2}{\rho_1}}\) ....(14)

This is another form of Graham's diffusion law.

Consider a gas enclosed in a cube. Let the axes be parallel to the sides of the cube (Fig.).

A molecule having velocity (V_x, V_y, V_z) hits the planar wall parallel to yz plane of area A(l²). As the collision is elastic, the molecule rebounds with the same velocity, y and z components of velocity do not change in the collision but the sign of x-component is reversed. Then, the velocity of collision is (-V_x, V_y, V_z). 

The change in momentum of molecule,

= -mV_x - (mV_x) = -2 mV_x ........(13)

According to the principle of conservation of momentum, the momentum imported to wall (in collision) = 2mV. Consider a small time interval ∆t, a molecule with velocity V_x will hit the wall when it is within the volume of AV_x ∆t and can hit the wall in time ∆t. The number of molecules with velocity (V_x, V_y, V_z) hitting the wall in time ∆t is AV_x ∆t n where n is the number of molecules per unit volume.

The total momentum transferred to wall by these molecules in time ∆t is:

\(Q = (2mV_x)(n\ AV_x\Delta t)\) 

The force on the wall is the rate of momentum transfer Q/∆t and pressure =  \(\frac{Force}{Area}\) 

\(\therefore\ P = \frac{Q}{A\Delta t}\) = n m V_x² 

There is a distribution in velocities. So, equation (13.11) stands for pressure due to the group of molecules having velocity V in x-direction and n is the number density of these molecules. 

The total pressure is

\(P = m\ n\overline{V_x^2}\ \)

Here \(\overline{V_x^2}\) is average of V_x².
If the gas is isotropic, i.e., the velocity of molecules in the vessel has no preferred direction.

So, by symmetry,

where V is speed and \(\overline{V^2}\) is the root mean square speed.

Remarks:

1. The shape of the vessel is immaterial. We always choose an infinitesimal (planar) area.

2. In the derivation, we have ignored many collisions. The number of molecules hitting the wall in time ∆t was n AV_x ∆t. The collisions are random and the gas is in a steady state. So, if a molecule having velocity (V_x, V_y, V_z) acquires a different velocity due to the collision with some molecule, then some other molecules with different initial velocity will acquire velocities (V_x, V_y, V_z) after collision. If it were not so, the distribution of velocities won’t be steady.