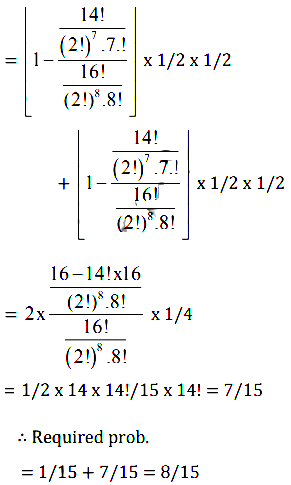Question

Sixteen players S₁, S₂ . . . . . . . . . . . . . . . . . . . S₁₆ play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players of the pair. Assume that all the players are of equal strength

(a) Find the probability that the player S₁ is among the eight winners. 

(b) Find the probability that exactly one of the two players S₁ and S₂ is among the eight winners. 

Answer 1

(a) Prob. of S₁ to among the eight winners = (prob. of S₁ being in a pair) x (prob. of S₁ winning in the group). 

= 1 x 1/2 [∵ S₁ is definitely in a group i.e. certain event] = 1/2 

(b) If S₁ and S₂ are in the same pair then exactly on wins. If S₁ and S₂ are in two pairs separately then exactly one of S₁ and S₂ will be among the eight winners if S₁ win and S₂ loses or S₁ loses and S₂ wins.

Now the prob. of S₁, S₂ being in the same pair and one wins. = (prob. of S₁, S₂ being in the same pair) x (prob. of any one winning in the pair) 

And the prob. of S₁, S₂ being in the same pair 

= n (E)/n (S), where n (S) = the no. of ways in which 16 person can be divided in 8 pairs; n (E) = the no. of ways in which S₁, S₂ are in same pair or 14 persons can be divided into 7 pairs. 

∴ n (E) = 14!/(2!)⁷ .7! and n (S) = 16!/(2!)⁸ .8! 

∴ Prob. of S₁ and S₂ being in the same pair 

= 14!/(21)⁷.7!)/(16!/(2!)⁸.8!

 = 21.8/16.15 = 1/15 

The prob. of any one winning in the pair of S₁, S₂ = P (certain event) = 1 

∴ The pair of S₁, S₂ being in two pairs separately and any one of S₁, S₂ wins. 

= the prob. of S₁, S₂ being in two pairs separately and S₁ wins, S₂ loses + the prob. of S₁, S₂ being in two pairs separately and S₁ loses, S₂ wins.