Question

If ρ₁ and ρ₂ be the radii of curvature at the ends of a focal chord of the parabola y² = 4ax, then show that ρ₁^–2/3 + ρ₂^–2/3 = (2a)^–2/3. 

Answer 1

The given parabola y² = 4ax passing through any general point P(x, y) in its parametric form is given as follows:

 x = at², y = 2at

so that x' = 2at, y' = 2a

            x'' = 2a, y'' = 0                                                              .....(1)

∴ ρ at P(x,y) = 

                                              .....(2)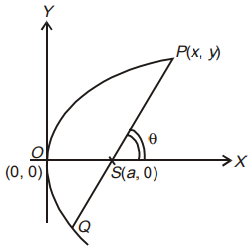

If ρ at P(x, y) is denoted by ρ₁, then

ρ₁ ^-2/3 = 

                                           .....(3)

Further, the parametric coordinates of point Q at the 2nd end of the focal chord would be

                              .....(4)

The general equation of the line passing though P(t₁) and Q(t₂) with parametric variables t₁ and t₂,

(t₁ + t₂)y = 2x + 2at₁t₂

But if it pass through S(a, 0) where x = a, y = 0, we get (t₁ + t₂) · 0 = 2a + 2a t₁t₂, i.e. t₂ = - 1/t₁

With above arguments, ρ at Q if denoted by ρ₂, then

                                            .....(5)

Adding (4) and (5), we get

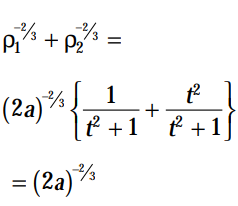
Hence the result.