Let r = 1/u ......(1)
so that for l/r = (1 + e cosθ) we get
and
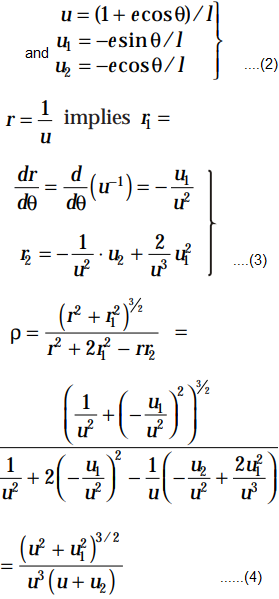
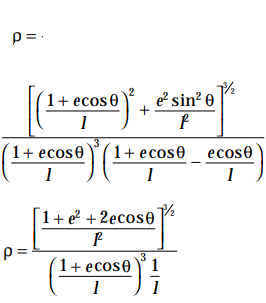 .....(5)
.....(5)
The general equation of the conic I/r = (1 + e cos θ) represents
a parabola for e = 1
an ellipse for e < 1
a hyperbola for e > 1
thus for e =1 , p =
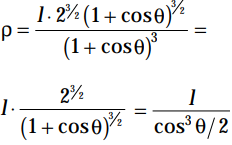 .....(6)
.....(6)
Now if ρ at P is termed as ρ1 and ρ at Q is termed as ρ2, then


Add the two, ρ1 –2/3 + ρ2 –2/3 = l –2/3