Question

Find the radius of curvature for the following curves

(i) rⁿ = aⁿcosnθ (ii) r = ae^θ·cotα (iii) r² = a² cos2θ

Answer 1

(i) Given rⁿ = aⁿcosnθ                                                                                     ......(1)

Taking logs on both sides

n log r = n log a + log cos nθ

Differentiating, n/r.dr/dθ = 0 + 1/ (cos nθ) x (- n sin nθ) , i.e. r₁ = –rtannθ           .....(2)

Again differentiating,

r₂ = – r n sec²nθ – r₁tan nθ = – r n sec²nθ + r tan²nθ                                                 ...(3)

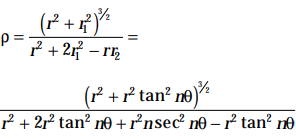
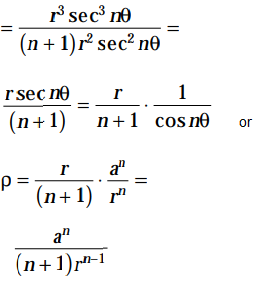
In other words, here ρ varies as the (n – 1)^th power of the radius vector.

Alternately: Change the given equation into its pedal form and then find r . dr/ dp

Here in this problem, dr/dθ = r₁ = - r tan nθ

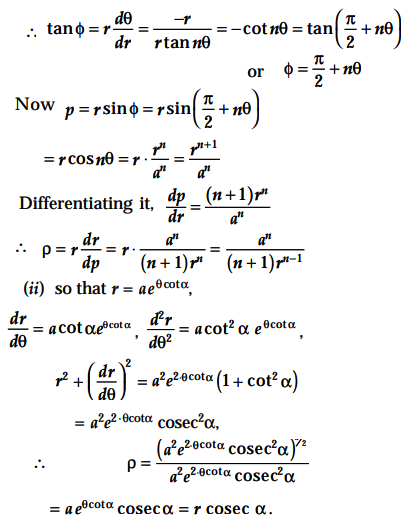
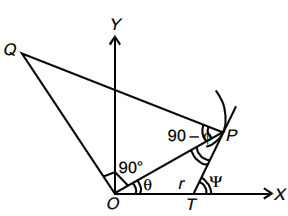
Extension: Show that in equiangular spiral r = a e^θcotα, radius of curvature subtends a right angle at the pole

Here 

(iii) Given r² = a²cos2θ                                                                                        ......(1)

Differentiating (1) with respect to θ, we get

r.dr/dθ = - a² sin 2θ                                                                                          .......(2)

Further differentiating with respect to θ, we get

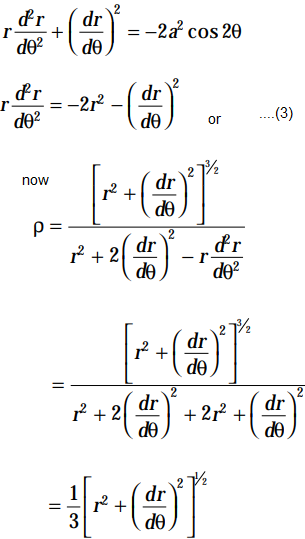                                               ......(4)

On squaring and adding (1) and (2), we get 

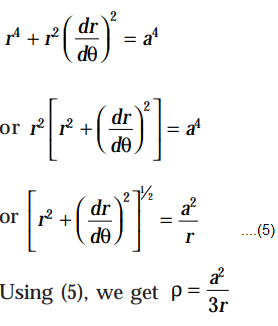
Corollary: Radius of curvature of the lemniscate r² = a²cos2θ at the point where tangent is parallel to X-axis is  √2a²/3. Here in this curve tangent and the radius vector coincides at θ = ±π/4. Therefore