Question

Find the area of the region bounded by the curves y = 3x²/4 and the line 3x – 2y + 12 = 0.

Answer 1

Given curves are y = 3x²/4 and 3x – 2y + 12 = 0

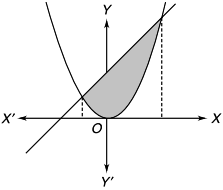
Hence, the required area

\(\int\limits_{-2}^4(y_2-y_1)dx\)  

= \(\int\limits_{-2}^4(\frac{3x+12}{2}-\frac{3x^2}{4})dx\)

= \(\frac{3}{4}\int\limits_{-2}^4(2x+8-x^2)dx\) 

= \(\frac{3}{4}(x^2+8x-\frac{x^3}{3})_{-2}^4\)

= \(\frac{3}{4}((16+32-\frac{64}{3})\) - \((4-16+\frac{8}{3}))\) 

= \(\frac{3}{4}(36-\frac{72}{3})\) 

= \(\frac{3}{4}(\frac{108-72}{3})\) 

= \(\frac{108}{4}\) 

= 27 sq.u.