Question

A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and base radius of the cone are also the same. Find the whole surface and volume of the remaining Cylinder.

Answer 1

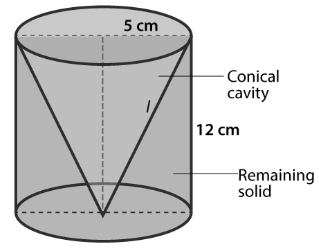
Given,

Height of the circular Cylinder (h₁) = 12 cm

Base radius of the circular Cylinder (r) = 5 cm

Height of the conical hole = Height of the circular cylinder, i.e., h₁ = h₂ = 12 cm

And, Base radius of the conical hole = Base radius of the circular Cylinder = 5 cm

Let’s consider, L as the slant height of the conical hole.

Then, we know that

Now,

The total surface area of the remaining portion in the circular cylinder (V₁) = πr² + 2πrh + πrl

V₁ = π(5)²  + 2π(5)(12) + π(5)(13)

V₁ = 210 π cm²     

And, the volume of the remaining portion of the circular cylinder = Volume of the cylinder – Volume of the conical hole

V = πr²h – 1/3 × 22/7 × r² × h

V = π(5)²(12) – 1/3 × 22/7 × 5² × 12

V = 200 π cm²