The sum or difference of two G.P.s, is again a G.P.

Question

State whether statement in True or False.

The sum or difference of two G.P.s, is again a G.P.

Answer 1

Let us consider two G.P’s

a, ar, ar², ar³, …, ar^n-1

and a₁, a₁r₁, a₁r₁², …, a₁r₁^n–1

Now, we will find the sum of these two G.Ps, we get

(a + a₁) + (ar + a₁r₁) + (ar² + a₁r₁²) + … + (ar^n-1 + a₁r₁^n-1)

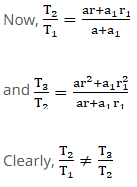
So, the sum of two G.Ps is not a G.P because the common ratio is not same.

Now, we will find the difference of the two G.Ps

(a – a₁) + (ar – a₁r₁) + (ar² – a₁r₁²) + … + (ar^n-1 – a₁r₁^n-1)

So, the difference of two G.Ps is not a G.P because the common ratio is not same.

Hence, the given statement is FALSE