If sin A = 3/5, 0 < A < π/2 and cos B = -12/13, π < B < 3π/2, find the values of the following: (i) cos(A + B)

Question

If sin A = \(\frac{3}{5}\), 0 < A < \(\frac{\pi}{2}\) and cos B = \(\frac{-12}{13}\), π < B < \(\frac{3\pi}{2}\), find the values of the following: 

(i) cos(A + B) 

(ii) sin(A – B) 

(iii) tan(A – B)

Answer 1

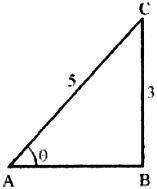
Given that sin A = \(\frac{3}{5}\), 0 < A < \(\frac{\pi}{2}\)(i.e., A lies in first quadrant)

Since A lies in first quadrant cos A is positive.

cos A = \(\frac{Adjacent\,side}{Hypotenuse}=\frac{4}{5}\)

tan A = \(\frac{3}{4}\)

AB = \(\sqrt{5^2-3^2}\) = 4

Also given that cos B = \(\frac{-12}{13}\), π < B < \(\frac{3\pi}{2}\)(i.e., B lies in third quadrant)

Now sin B lies in third quadrant. sin B is negative.

CA = \(\sqrt{13^2-12^2}=5\)

sin B = \(\frac{-opposite\,side}{Hypotenuse}=\frac{-5}{13}\)

tan B = \(\frac{-opposite\,side}{Adjacent}=\frac{5}{12}\)

[B lies in 3rd quadrant. tan B is positive.] 

(i) cos(A + B) = cos A cos B – sin A sin B

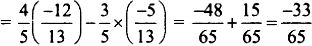
(ii) sin(A – B) = sin A cos B – cos A sin B

(iii) tan(A – B)