Question

Find the values of a and b for which the system of linear equations has an infinite number of solutions: 

2x - 3y = 7, (a + b)x - (a + b – 3)y = 4a + b.

Answer 1

The given system of equations can be written as 

2x - 3y = 7 

⇒2x - 3y - 7 = 0 ….(i) 

and (a + b)x - (a + b – 3)y = 4a + b 

⇒(a + b)x - (a + b – 3)y - 4a + b = 0 ….(ii) 

These equations are of the following form: 

a₁x+b₁y+c₁ = 0, a₂x+b2y+c₂ = 0 

Here, a₁ = 2, b₁= -3, c1 = -7 and a₂ = (a + b), b₂ = -(a + b - 3), c₂ = -(4a + b) 

For an infinite number of solutions, we must have:

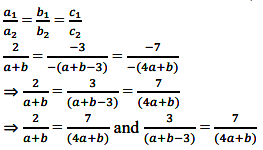
⇒ 2(4a + b) = 7(a + b) and 3(4a + b) = 7(a + b - 3) 

⇒ 8a + 2b = 7a + 7b and 12a + 3b = 7a + 7b - 21 

⇒ 4a = 17 and 5b = 11 

∴ a = 5b …….(iii) 

and 5a = 4b – 21 ……(iv) 

On substituting a = 5b in (iv), we get:

25b = 4b – 21 

⇒21b = -21 

⇒b = -1 

On substituting b = -1 in (iii), we get: 

a = 5(-1) = -5 

∴a = -5 and b = -1.