Given,
|x+1|+|x|>3
Subtracting 3 from both sides, we get –
|x+1|+|x|–3>0
For this, we have 3 cases,
Case 1 : –∞ < x < -1
For this,
|x+1| = –(x+1) and |x| = –x
–(x+1)–x–3>0
–2x–1–3>0
2x+4<0
x<–2
⇒ x ∈ (–∞,–2) …(1)
Case 2 : –1 < x < 0
For this,
|x+1| = x+1 and |x| = –x
x+1–x–3>0
–2>0
Which is absurd, thus it leads to no solution.
Case 3 : 0< x< ∞
For this,
|x+1| = x+1 and |x| = x
x+1+x–3>0
2x–2>0
x>1
⇒ x ∈(1 ,∞) …(2)
⇒ x∈ (–∞,–2)⋃ (1 ,∞) (from 1 and 2)
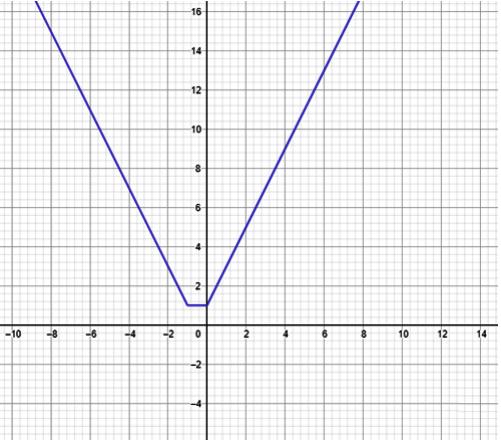
We can verify the answers using graph as well.