Evaluate the following limit : lim(x→-1) (x^3 + 1)/(x + 1)

Question

Evaluate the following limit : \(\lim\limits_{\text x \to 1}\cfrac{\text x^3+1}{\text x+1} \)

lim(x→-1) (x³ + 1)/(x + 1)

Answer 1

We need to find the limit for : \(\lim\limits_{\text x \to 1}\cfrac{\text x^3+1}{\text x+1} \)

As limit can’t be find out simply by putting x = –1 because it is taking indeterminate form(0/0) form, so we need to have a different approach.

Let, Z = \(\lim\limits_{\text x \to 1}\cfrac{\text x^3+1}{\text x+1} \)

Note: To solve the problems of limit similar to one in our question we use the formula mentioned below which can be derived using binomial theorem.

Formula to be used: \(\lim\limits_{\text x \to a}\cfrac{(\text x)^n-(a)^n}{\text x-a} \) = na^{n -1}

As Z does matches exactly with the form as described above so we don’t need to do any manipulations–

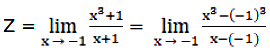
Use the formula: \(\lim\limits_{\text x \to a}\cfrac{(\text x)^n-(a)^n}{\text x-a} \) = na^{n -1}

∴ Z = 3(–1)^3–1 = 3

Hence, \(\lim\limits_{\text x \to 1}\cfrac{\text x^3+1}{\text x+1} \) = 3