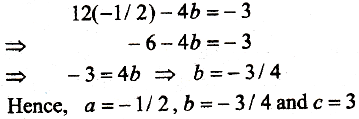Question

The curve y = ax³ + bx² + cx + 5, touches the x-axis at P(-2, 0) and cuts they axis at a point Q, where its gradient is 3. Find a, b, c.

Answer 1

Given that y = ax³ + bx² + cx + 5 touches x-axis at P(-2, 0)which implies that x-axis is tangent at (-2, 0) and the curve is also passes through (1, 0).

The curve cuts y-axis at (0, 5) and gradient at this point is given 3, therefore at (0, 5) slope of the tangent is 3.

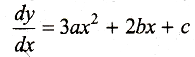
Since, x-axis is tangent at (-2,0), therefore.

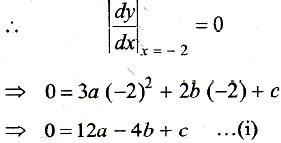
Again, slope of tangent at (0, 5) is 3

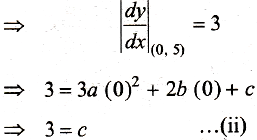
Since, the curve passes through (-2, 0), we get

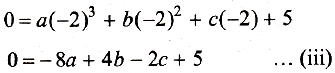
From Eqs. (i) and (ii), we get

2a - 4b = -3 .....(iv)

From Eqs. (iii) and (ii), we get

-8a + 4b = 1 ....(v)

On adding Eqs. (iv) and (v), we get

4a = -2

a = -1/2

On putting a = - 1/2 in Eq. (iv), we get