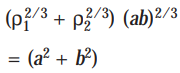Question

If ρ₁, ρ₂ be the radii of curvature at the extremities of two conjugate semi diameters of an ellipse, prove that (ρ₁^2/3 + ρ₂^2/3) (ab)^2/3 = (a² + b²)

Answer 1

Clearly in the geometry, CP and CD are two conjugate semi-diameters to each other to the ellipse with a and b as the semi-major and semiminor axis respectively. 

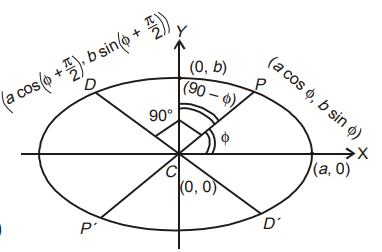
Thus for P(x,y),

x = a cos φ

y = b sin φ                                                                         ......(1)

we get  x' = dx/dφ = - a sin φ

and y' = b cos φ

and x'' = d²x/ dφ² = - a cos φ and y" = - b sin φ                   ......(2) 

∴  Radius of curvature at P(x, y), 

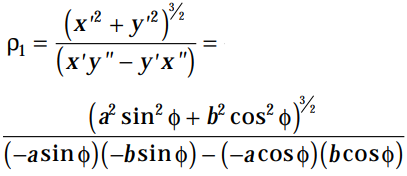
                  ......(3)

Now for position D radius vector CD encloses an angle (90 + φ) with the initial axis (instead φ as in case of P) Therefore, radius of curvature at D

p₂ =

    ........(4)

Whence

that is