Question

Two concentric circles have radius 5 cm and 3 cm respectively. Find the length of chord of circle which touches the smaller circle.

Answer 1

Let two concentric circle with center O.

Let radius OA and OP are 5 cm and 3 cm respectively.

AB is the chord of bigger circle which touches smaller circle at point P.

∴ OP ⊥ AB 

∠OPA = 90°

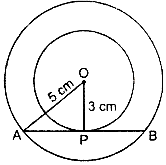
∴ In right angled ∆OPA, by Pythagoras theorem.

AP² + OP² = OA²

⇒ AP² + (3)² = (5)²

⇒ AP² = (5)² – (3)²

= 25 – 9 = 16

∴ AP = 4 cm

But in bigger circle, OP is perpendicular to chord AB from center O.

∴ Point P bisects the chord AB.

AP = BP = 4 cm

Length of chord AB = AP + BP

= 4 + 4 = 8 cm

So, Length of chord of bigger circle = 8 cm.