Given :
A quadrilateral PQRS circumscribes a circle with center O. Sides of quadrilateral PQ, QR, RS and SP touches the circle at point L, M, N, T respectively.
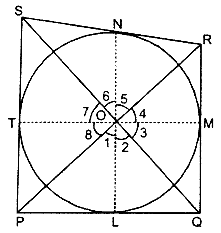
To prove : ∠POQ + ∠SOR = 180°
and ∠SOP + ∠ROQ = 180°.
Construction : Join P, Q, R, L, M, N and T with center O of circle.
Proof: Since, OL, OM, ON and OT are radius of circle and QL, MQ, RN and ST are tangents of circle.
So
QL ⊥ OL, QM ⊥ OM, RN ⊥ ON and ST ⊥ OT
Now in right angled ΔOMQ and right ΔOLQ
∠OMQ = ∠OLQ (each 90°)
hypotenuse OQ = hypotenuse OQ (common side)
and OM = OL (equal radii of circle)
∴ OMQ = OLQ (By RHS Congruence)
⇒ ∠3 = ∠2 (CPCT)
Similarly ∠4 = ∠5
∠6 = ∠7 and ∠8 = ∠1
∵ Sum of all angles made on point O of center of circle = 360°.
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
⇒ ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
⇒ 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180°
∠POQ + ∠SOR = 180°
[ ∵∠1 + ∠2 = ∠POQ and ∠5 + ∠6 = ∠SOR ]
Similarly ∠SOP + ∠ROQ = 180°
So, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of circle.