Question

Two circles with radii ‘a’ and ‘b’ respectively touch each other externally. Let ‘c’ be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then, 

(a) \(\frac{1}{\sqrt{a}}\)- \(\frac{1}{\sqrt{b }}\) = \(\frac{1}{\sqrt{c}}\)

(b)  \(\frac{1}{\sqrt{a}}\)- \(\frac{1}{\sqrt{b}}\) = \(\frac{-1}{\sqrt{c}}\)

(c) \(\frac{1}{\sqrt{a}}\) + \(\frac{1}{\sqrt{b}}\) = \(\frac{1}{\sqrt{c}}\) 

(d) None of these

Answer 1

Answer : (c) \(\frac{1}{\sqrt{a}}\) + \(\frac{1}{\sqrt{b}}\) = \(\frac{1}{\sqrt{c}}\) 

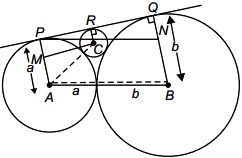
Let the centres ofthe three circles with radii a, b, c be A, B and C respectively. Let the common tangent touch the three circles at points, P, Q and R respectively.

Since radius ⊥ tangent at point of contact 

∠ APR = ∠ CRQ = ∠BQR = 90° 

Draw a line CM || PR meetingAP in M. Then, ∠AMC = 90° 

∴ CM = PR and MP = CR and AM = AP – MP = a – c and AC = a + c

( ∴ In rt ∆ AMC, MC = \(\sqrt{AC^2-AM^2}\) = \(\sqrt{(a+c)^2 -(a-c)^2}\)  = 2\(\sqrt{ac}\) ) 

Similarly we can show that RQ =  2\(\sqrt{bc}\) 

⇒ PQ = PR + RQ =  2\(\sqrt{ac}\)  +  2\(\sqrt{bc}\)   ... (i)

Also, draw a line from P || AB meeting BQ in N. 

Then, PN = AB = a + b, 

QN = BQ – BN = b – a

In rt. ∆ PQN, PQ = \(\sqrt{PN^2-QN^2}\) 

= \(\sqrt{(a+b)^2 -(a-b)^2}\) = 4ab

⇒ PQ =  2\(\sqrt{ab}\)  ...(ii)

From (i) and (ii) 

 2\(\sqrt{ac}\)  +  2\(\sqrt{bc}\)  =  2\(\sqrt{ab}\)  

⇒   \(\frac{1}{\sqrt{a}}\) + \(\frac{1}{\sqrt{b}}\) = \(\frac{1}{\sqrt{c}}\)